LA TECNOLOGÍA AL ALCANCE DE TODOS

En el siguiente enlace puedes ver los apuntes de clase.

En la parte superior,  puedes ver una tabla con los apuntes que el profesor entrego en la clase.

Acontinuación, voy a colocar una serie de videos donde puedes ver un repaso a las explicaciones de los problemas realizados en clase.

Esta sección de mecanismos está dividido en 2 bloques:

1. Sentido de giro de todos los tipos de mecanismos. (Fijate en el apartado 1, es un ejemplo de una actividad).

2. Realización y repaso de las actividades de poleas con correa, ruedas de fricción, engranajes, aplicación de una bicicleta y la relación de transmisión.

1.Sentido de giro de cada una de las poleas, engranajes ....

1.2.  Mecanismos transmisión por correa 

2. Realización y repaso de las actividades.

Información obtendia del canala de youtube de Ruben Sebastian https://www.youtube.com/user/rbnterrassa


2.1 Transmisión por Poleas con Correas

2.2 ¿Qué son los engranajes? Rueda motriz y conducida. 
Fórmulas

Las explicación son muy interesantes pero tienes que cambiar los datos siguientes por los empleados en la clase:

W por N es la velocidad de la rueda de fricción o engranaje en rpm (revoluaciones por minuto)

r por i es la relación de transmisión, es un valor adimensional al no tener unidades.

Z representa el número de dientes.

d representa el díametro de la rueda de fricción o de las poleas unidas por una correa.

Todos los problemas explicados en la parte inferior sirven para el caso de poleas unidas por correa o ruedas de fricción, pero cambiando la Z de los engranajes por la d de las poleas o ruedas de friccion.

Formulas que vamos usar en nuestros problemas:

2.3. PROBLEMA EXPLICADO PASO A PASO:  
¿En qué sentido giran las ruedas de un engranaje?

Vamos a realizar un ejercicio para ver el sentido de giro de cada uno de los engranajes

2.4. PROBLEMA EXPLICADO PASO A PASO:  
Transmisión por Poleas con Correas

En una transmisión por correa, la polea motriz o conductora tiene un diámetro de 400 mm y la polea conducida de 120 mm.

a) Si la motriz está conectada a un motor que gira a 800 rpm, ¿cuántas vueltas dará un ventilador que está montado en el eje de salida?

b) Por cada vuelta de la motriz, ¿cuántas da la conducida?

c) ¿Qué tipo de transmisión es: igualdad, reducción o aumento de velocidad?

2.5. PROBLEMA EXPLICADO PASO A PASO:  
Engranaje reductor o multiplicador. Número de vueltas de las ruedas.

 Veremos como saber si un engranaje es multiplicador o reductor a partir de un dibujo o del número de dientes, y aprenderemos a calcular el número de vueltas que da una rueda en función de la otra.

1. Si la rueda motriz es la de la izquierda, indica si se produce multiplicación, reducción o se mantiene el movimiento.

2. Encuentra la relación de transmisión entre dos ruedas de un engranaje donde la motriz tiene 15 dientes y la conducida 25 dientes. Si la rueda motriz hace 8 vueltas, ¿cuántas dará la rueda conductora?

3. En una transmisión por engranajes, la rueda motriz tiene 24 dientes y la conducida 18. ¿Será un sistema reductor o multiplicador? ¿Cuántas vueltas ha de dar la rueda motriz para que la conducida haga 30 vueltas completas?

2.6. PROBLEMA EXPLICADO PASO A PASO:

 Engranaje reductor o multiplicador. Número de vueltas de las ruedas.

 4. ¿Cuántos dientes ha de tener una rueda dentada motriz que gira a 20 rad/s y que estará engranada a otra rueda dentada de 16 dientes y una velocidad de giro de 10 rad/s? ¿El sistema es reductor o multiplicador? ¿Hay cambio en el sentido del giro en el segundo engranaje?

5. Considera un engranaje con dos ruedas de 20 y 25 dientes respectivamente. Si la primera, que es la rueda motriz, gira a una velocidad de 10 rad/s, calcula a qué velocidad angular gira la otra rueda. ¿Cambia el sentido de giro? a. Si ponemos en medio otra rueda de 40 dientes, ¿a qué velocidad se movería ahora el tercer engranaje? ¿Qué cambiaría?

2.7. PROBLEMA EXPLICADO PASO A PASO:  
Engranaje reductor o multiplicador. Número de vueltas de las ruedas.

 6. ¿Cuántos dientes ha de tener una rueda dentada motriz que gira a 1500 rpm y que estará engranada a otra rueda dentada de 16 dientes y una velocidad de giro de 1875 rpm? ¿El sistema es reductor o multiplicador? ¿Hay cambio en el sentido del giro en el segundo engranaje?

7. Considera un engranaje con dos ruedas de 20 y 25 dientes respectivamente. Si la primera, la motriz, gira a una velocidad de 700 rpm, calcula a qué velocidad angular gira la otra rueda. ¿Cambia el sentido de giro? a. Si ponemos en medio otra rueda de 40 dientes, ¿a qué velocidad se movería ahora el tercer engranaje? ¿Qué cambiaría?

2.8. PROBLEMA EXPLICADO PASO A PASO:  
Engranaje reductor o multiplicador. Número de vueltas de las ruedas.

Explicaremos paso a paso como resolver dos problemas de trenes de engranajes, y además los resolveremos de diferentes maneras.

9. Tenemos tres engranajes como los de la figura. Determina la velocidad de la rueda de salida C. a. Si la rueda C fuese de 15 dientes, ¿sería un sistema multiplicador o reductor?

10. Tenemos un tren de engranajes como el de la figura. La rueda motriz, la de la izquierda, tiene una velocidad de 1500 rpm y 15 dientes. Si la central tiene 25 dientes, ¿cuántos dientes ha de tener la última rueda para que le lleguen 450 rpm?

2.9. PROBLEMA EXPLICADO PASO A PASO:  
Engranaje reductor o multiplicador. Número de vueltas de las ruedas.
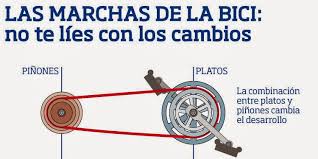
Caso partícular de una bicicleta de carreras

Z1 es el plato situado en la zona de los pedales: es el engranaje motríz o conductor.

Z2 es el piñón situado en la rueda trasera: es el engranaje conducido

Calcularemos la relación entre los platos y los piñones de una bicicleta, cuántas vueltas darán los piñones por cada pedaleada o vuelta de los platos. Y además veremos cuántos metros recorrerá la rueda con cada pedaleo.

8. Una bicicleta tiene dos platos de 40 y 52 dientes, y cuatro piñones de 15, 18, 21 y 24 dientes. Calcula las vueltas que dará la rueda trasera por cada pedaleo en las siguientes situaciones:

a. Con el plato grande y el piñón pequeño.

b. Con el plato pequeño y el piñón de 21.

c. Con el plato pequeño y el piñón grande.

No entra en los ejercicios de clase o exámenes las explicaciones el apartado del video desde el minuto 2 segundos 48

d. Si la rueda hace 622 mm de diámetro,

¿cuántos metros hará el ciclista con las combinaciones anteriores, por cada pedalada?

3. Actividades.

1. Bloque de actividades Nº: 1 (desde el problema nº 24)

2. Bloque de actividades Nº: 2 (desde el problema nº 21)

3. Bloque de actividades Nº: 3 (desde el problema nº 17)

4. Bloque de actividades Nº: 4 + teoría (desde el problema nº 26)